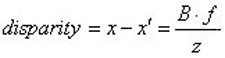[13호]스테레오 영상을 처리하는데 있어 발생하는 이슈
스테레오 영상을 처리하는데 있어발생하는 이슈글 | 위드로봇(주) 김도윤 ■ 스테레오 비전이란? 영화관에서 3D나 4D라는 표현이 자주 쓰이게 되면서 입체감 있는 영상에 대한 이해는 예전보다는 훨씬 쉬워졌습니다. 일반 카메라로 찍은 사진은 3차원(3D) 물체의 반사광을 2차원(2D) 필름 또는 2차원 센서에 투영(projection) 시킨 것이기에 3차원 정보 중 카메라에서부터 물체까지의 거리 정보는 사라지게 됩니다. 즉 3D가 2D로 바뀌게 되고 이러한 과정을 projection 이라고 하는 것이죠. 따라서 한 장의 사진으로는 이러한 거리 정보는 알아낼 수가 없습니다. 이건 간단한 실험으로도 확인해 볼 수 있습니다. 공을 던졌다 잡을 때 한 쪽 눈을 감고 던졌다 잡으려고 해 보면 공과 거리감이 사라져 잡기가 매우 어렵다는 것을 경험할 수 있습니다. 사라진 거리 정보를 복원하기 위해서는 또 다른 위치에서 찍은 다른 사진이 필요하게 되죠. 이 때문에 사람의 눈도 두 개가 있어 같은 물체를 서로 다른 장소(양쪽 각각의 눈 위치)에서 보고 그 영상의 차이를 이용해 거리를 복원하고 있습니다. 따라서 영상을 통해 거리 정보를 파악하고 카메라는 한 대가 아닌 두 대 이상이 되어야만 합니다. 이처럼 “같은 물체에 대해 서로 다른 장소에서 촬영한 여러 이미지에서 물체의 3차원 정보를 계산하는 학문 분야”가 바로 스테레오 비전입니다. 각각은 다시 여러 제한 조건들에 따라 카메라 캘리브레이션이 되어 있는지 아닌지(calibrated or uncalibrated), 카메라를 하나를 사용하고 이를 움직여가며 촬영하는 방식인지, 아니면 여러 대의 카메라를 사용하는 것인지(isolated camera or video sequence), 이미지가 단순히 두 장인지 아니면 수 십, 수 백장을 처리하는 시스템인지에 따라 다양한 연구가 진행됩니다. 하지만 좁은 의미에서는 서로 다른 장소에서 촬영한 두 장의 이미지에서 거리 정보를 추출해 내는 분야로 이해되기도 합니다. ■ 거리 정보란?
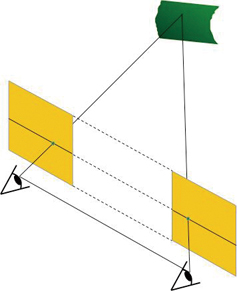
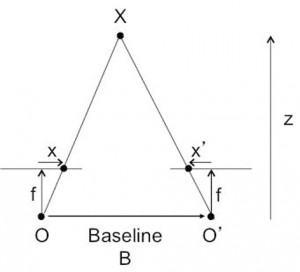
위 사진은 특정 건물을 위치를 조금 달리해서 찍은 두 장의 사진입니다. 얼핏 보면 같아 보이지만 자세히 보면 조금 틀리다는 것을 알 수 있습니다. 가까이 있는 좌측 건물 지붕에 비해 뒤에 있는 더 멀리있는 나무의 위치는 두 장의 이미지에서는 확연히 차이가 나는 부분입니다. 이처럼 동일한 물체에 대한 두 장의 사진 사이에서 나타나는 차이점을 이용하면 이미지 중에서 어느 부분이 카메라를 기준으로 더 가까운지를 알아낼 수 있습니다. 이를 이미지나 거리값으로 계산한 결과를 거리 정보라고 합니다. 2차원 이미지 형태로 나타내는 것이 직관적으로 파악되기에 위 그림에 대한 거리 정보는 아래 그림처럼 가까운 곳은 밝은 색으로 먼 곳은 어두운 색으로 표시하는 것이 일반적입니다. 자세히 보시면, 건물 앞에 있는 도로는 카메라 기준으로 가깝기에 밝은 색으로 표시되어 있고, 건물은 뒤쪽으로 갈수록 어두운 색으로 표시된 것을 확인할 수 있습니다. ■ 거리 정보와 디스패리티(Disparity)의 관계 앞서 살펴본 바와 같이 거리 정보를 파악하기 위해서는 양쪽 이미지 사이에 대응되는 점이 얼마나 차이가 나야 하는지를 파악했어야 했습니다. 이를 그림으로 그려보면 아래 그림처럼 3차원 공간 상의 한 점은 왼쪽, 오른쪽 눈에 각각 투영이 되는데 그 점의 거리에 따라 위치가 서로 다르게 됩니다. 가까이에 있는 물체는 그 차이가 크고, 멀리 있는 물체는 그 차이가 적게 되죠.
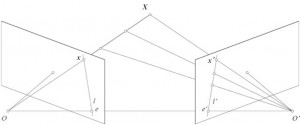
극단적으로 매우 멀리에 있는 물체는 차이가 나지 않게 됩니다. 이처럼 왼쪽 영상의 한 점의 위치에 비해 오른쪽 영상의 대응점 위치의 차이를 디스패리티(disparity)라 부르며, 그 관계식은 아래와 같습니다. 풀어서 설명해 보면 ‘왼쪽 영상 한 점의 위치에서 대응되는 오른쪽 영상 한 점의 위치 차이는 그 점의 3차원 공간 상의 거리 z에 반비례하며, 촛점 거리 f와 두 영상을 촬영할 때 거리차 B(베이스라인)에 비례한다’ 입니다. 예를 들어볼까요. 스테레오 카메라로 어떤 물체를 촬영해 보면, 가까이에 있는 물체는 왼쪽 영상과 오른쪽 영상에 그 차이가 두드러지게 나타나고, 멀리 있는 물체는 차이가 상대적으로 작게 나타나게 됩니다. 왼쪽 카메라와 오른쪽 카메라의 거리가 멀면 디스패리티가 크게 나타나기에 거리 정보를 보다 정밀하게 파악할 수 있습니다. 따라서 특정 스테레오 카메라로 거리 정보를 추출했는데 해상도가 불만족스럽고 더 높은 정밀도가 필요하다면 카메라와 카메라 사이를 넓히는 것도 한 가지 해결 방법이 됩니다. 또 다른 방법으로는 카메라 렌즈를 촛점 거리가 긴 모델로 바꾸는 것도 한 가지 방법이 되겠죠. 대신 베이스라인이 길어지거나 촛점 거리가 긴 모델로 바꾸면 한 번에 거리 정보를 계산할 수 있는 3차원 공간 상의 영역은 줄어들게 됩니다. 따라서 스테레오 비전을 연구하는 사람은 베이스라인이나 렌즈의 촛점 거리를 바꾸어 가며 자신의 실험에 가장 적절한 범위를 찾아야 할 필요가 있습니다. ■ 문제는 매칭(matching)이야! 지금까지 진행한 내용을 정리해볼까요? 한 대의 카메라로 찍은 한 장의 영상으로는 거리 정보를 알 수가 없었습니다. 그래서 두 대의 카메라(stereo camera)로 찍은 두 장의 영상에서 거리 정보를 추출해야하고, 거리 정보는 두 영상에서 대응되는 점의 위치가 서로 다르게 나타나며(disparity) 그 정도는 거리에 반비례해서 나타났었습니다. 디스패리티를 계산하면 거리 정보는 나오는 셈인데, 그럼 왼쪽 이미지의 한 점이 오른쪽 이미지 상 어디에 존재하는지를 찾아야 합니다. 이를 스테레오 비전에서는 매칭(matching) 또는 코레스펀던스(correspondence)라고 부릅니다. 얼핏 생각하면 매칭은 간단해 보이지만, 640×480 해상도를 가지는 VGA급 영상에서 예를 들어보면 다음과 같이 어마어마한 연산량을 필요로 합니다. (1) 왼쪽 이미지에서 한 점을 선택합니다. (2) 이 이미지와 같은 점은 오른쪽 이미지에서 640 x 480 loop를 돌려 찾습니다. (3) 다시 왼쪽 이미지에서 또 한 점을 선택하고 (2)를 반복합니다. 이러한 반복은 640×480번 반복됩니다. 어떻습니까? VGA급 영상은 최근 수M ~ 수 십M급 카메라에 비하면 매우 열악한 낮은 해상도임에도 불구하고, 매칭하는데 (640×480)x(640×480) 루프를 반복해야만 합니다. 당연히 시간이 많이 소요되고 실시간으로 계산이 안되게 됩니다. 또한 왼쪽 영상과 오른쪽 영상의 매칭을 하기 위해서는 한 점의 정보만으로는 부족한 경우가 태반이기에 매칭을 할 때는 일정 블록(block)을 이용하게 되며, 이 또한 연산 시간을 더욱 늘리게 됩니다. 따라서 스테레오 비전 분야의 연구 중에서 가장 중요한 부분은 바로 매칭 부분이며, 역설적이게도 많은 연구자들이 연구를 진행하고 있지만 아직까지 상업적으로 사용하기에는 많은 부분이 부족하기도 합니다. ■ 매칭 시간을 줄여주는 에피폴라 제한조건 (epipolar constraint) VGA급 해상도의 영상에서 거리를 추출하는데 1~2분씩 소요된다면 멈춰있는 물체의 경우에는 상관이 없을 수도 있지만 움직이는 로봇이라던지 자동차라면 전혀 사용할 수 없게 됩니다. 위 매칭 문제를 잘 살펴보면 왼쪽 영상에서 한 점에 대응되는 점을 찾기 위해 오른쪽 영상을 모두 뒤지고 있는 것을 발견할 수 있습니다. 물론 오른쪽 영상에 어디에 있는지는 미리 알 수 없기에 뒤져야 하는 것은 맞는데, 오른쪽 영상을 모두 뒤질 필요가 있을까요? 영상을 촬영할 때 카메라가 어떻게 배치되어 있는지 정보를 사전에 알 수 있다면 위 질문에 대한 답을 할 수가 있습니다. 이러한 내용이 담겨져 있는 수학적 정리가 에피폴라 제한조건입니다. 따라서 스테레오 매칭 문제에서 연산 속도를 증가시키기 위해서는 에피폴라 제한조건을 이해해서 이를 적용해야 하며, 이를 적용하면 2D 공간를 뒤져야 하는 일에서 1D 공간을 뒤지는 문제로 바꿀 수 있습니다. 에피폴라 제한조건은 Project Space에서 수학적으로 유도하면 깔끔하게 나오는 수식입니다만, 본고에서는 수식을 사용하지 않고 그림을 통해 물리적 의미를 전달해 보도록 하겠습니다. 자, 위 그림을 찬찬히 잘 살펴보겠습니다. 3차원 공간 상에 X라는 점이 있습니다. 이 점은 왼쪽 카메라에서는 렌즈 촛점 O와 연결하는 레이(ray)상에 놓이게 되므로 x로 투영됩니다. 위 그림에서 x를 확인하셨나요? 자, 그럼 이 부분이 매우 중요한데요, 이미지 상에서 본 x라는 점은 3차원 공간 상에 위치한 X이기도 하지만 xX 선분 상에 있는 어떠한 점도 영상에서는 x로 보이게 됩니다. 이게 앞서 설명한 “투영(projection)이 되기 때문에 영상에서 거리 정보는 없어진다”와 일맥상통한 부분이죠. 따라서 영상에서 x라는 점은 3차원 공간 상에서는 xX 라인에 있는 어떠한 점도 x가 될 수 있기에, x에 대응되는 오른쪽 카메라에서의 후보군은 선분으로 나타나게 됩니다. 이 때 이 선분들이 하나로 만나는 점이 생기는데요, 그 점은 재미있게도 왼쪽 카메라와 오른쪽 카메라의 중심(OO’)을 서로 연결한 직선이 이미지를 관통하는 점 e와 e’ 으로 나타납니다. 이 때 파악된 e를 에피폴(epipole)이라고 부르고 에피폴을 지나는 후보군 선분을 에피폴라 라인(epipolar line)이라고 부릅니다. 그리고 이러한 일련의 조건들을 에피폴라 제한조건이라고 합니다. 이 부분은 매우 중요하니 설명과 그림을 보면서 충분히 숙지하시기 바랍니다. 우리가 매칭에 활용한 부분은 에피폴라 라인입니다. 다시 거슬러올라가 볼까요? (a)거리 정보를 알기 위해서는 디스패리티 파악이 필요했습니다. (b)디스패리티를 알기 위해서는 매칭을 해야 하는데, 매칭은 영상 전체를 모두 뒤져야 하기 때문에 매우 연산량이 많았습니다. (c)그런데 앞서 본 바에 의하면 왼쪽 영상에서 한 점은 3차원 공간 상에서 후보군이 한 직선으로 나타나고 이는 오른쪽 카메라에서 특정한 라인으로 표시가 되는데, 그 라인은 항상 에피폴을 지나갔었습니다. (d)에피폴은 카메라 배치에 따라 정해지는 것이므로 미리 알 수가 있으니 이를 이용하면 오른쪽 영상 전체를 뒤질 필요없이 에피폴라 라인만 뒤지면 됩니다. (e) 그럼 이제 에피폴을 어떻게 찾아내는가 문제로 바뀝니다. ■ 스테레오 카메라 캘리브레이션 에피폴은 각각의 카메라 중심을 연결한 선이기에 카메라 중심을 정확하게 알아야 할 필요가 있습니다. 이는 다시 카메라 캘리브레이션으로 해결하는 문제로 바뀝니다. 카메라 캘리브레이션은 그 자체만으로도 또 하나의 중요한 학문 분야여서 원론부터 설명하면 매우 길어집니다. 본고는 스테레오 카메라에서 발생하는 문제에만 관심을 집중해 보겠습니다. 다행히도 스테레오 카메라의 캘리브레이션을 위한 기법들은 오픈 소스로 많이 공개되어 있으며, 라이브러리로도 공급이 됩니다. 대표적으로 유명한 라이브러리는 OpenCV이며, 이 안에는 Jang이 만든 캘리브레이션 기법이 구현되어 있습니다. 미리 준비된 체크 무늬 PDF 문서를 프린터로 출력하여 카메라 앞에서 이 출력 문서를 움직여가며 촬영한 이미지를 캘리브레이션 프로그램에 넣어주면 스테레오 카메라 캘리브레이션 결과값인 펀더맨털 행렬(Fundamental matrix)를 결과값으로 반환합니다. 이 값을 이용하면 2D 공간을 모두 뒤지던 매칭 문제를 1D 공간 문제로 바꿀 수 있으며, 이 또한 OpenCV에 이러한 기법으로 구현된 함수와 예제 코드가 있습니다. ■ 에피폴라 라인을 일치시키는 렉티피케이션(rectification) 스테레오 카메라 캘리브레이션이 완료되면 에피폴의 위치를 알 수 있고 왼쪽 카메라 한 점에 대응되는 오른쪽 카메라 영상의 에피폴라 라인을 알 수 있습니다. 일반적인 스테레오 카메라에서는 아래 그림처럼 에피폴라 라인이 사선으로 나타나게 됩니다. 이제 이 에피폴라 라인만 뒤지면 매칭 문제는 해결할 수 있는데, 문제는 이 라인을 뒤지는 것도 일입니다. X 축으로 평행한 평행선이 아니기에 일일히 다음 점의 위치를 찾아 이미지 값을 확인해야 하는 식으로 프로그래밍이 됩니다.
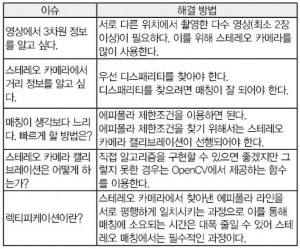
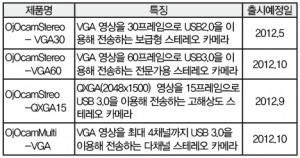
이렇게 변환해 놓으면, 왼쪽 영상의 한 점은 오른쪽에서 한 줄만 처음에서부터 끝까지 쭉 찾으면 되기에 프로그램 코드가 무척 간결해 집니다. 물론 이렇게 렉티피케이션하는데 시간은 추가로 소요되지만 매칭에 줄어드는 시간까지 함께 생각해 보면 렉티피케이션을 수행하는 쪽이 더 빠르기에 스테레오 매칭에 있어서 렉티피케이션은 필요한 과정으로 인식되고 있습니다. 스테레오 카메라에 따라서 이러한 렉티피케이션까지 수행한 결과를 출력하는 스테레오 카메라도 있습니다. 이러한 카메라를 사용하면 프로그램에서는 알고리즘에 사용할 수 있는 시간이 더 많이 확보되기에 고급 알고리즘을 구현하는데 부담을 덜 수 있다는 장점이 생기죠. ■ 이슈 정리 스테레오 영상을 처리하는데 발생하는 이슈들을 시간 순으로 열거해 보았고 각각은 어떻게 해결해야 하는지를 설명했습니다. 간략히 표로 정리하면 다음과 같습니다. ■ 스테레오 카메라 OjOcamStereo-VGA30
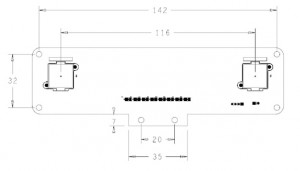
위에 언급했듯이 영상으로 3차원 정보를 찾아내는 문제는 많은 응용 분야가 있기에 위드로봇 연구소에서는 스테레오 영상에 관련된 많은 용역을 수행했었습니다. 일부는 스테레오 카메라를 만드는 일도 있었고, 일부는 스테레오 카메라는 기존 상용품을 사용하되 처리 알고리즘을 개발하는 업무이기도 했습니다. 후자의 경우 대표적인 상용품이 몇 가지 있는데 무척 고가(5백만원 ~ 수 천만원)에 판매되고 있습니다. 위드로봇 연구소에서도 연구에 활용하기 위해 구매하여 사용하고 있습니다만 매우 비싸기에 여러 명이 돌려가며 사용하고 있는 형국입니다. 그래서 스테레오 카메라 제작 및 영상 처리 알고리즘 기술은 확보되었기에 위드로봇 연구소 내부에서 쓸 목적으로 처음에는 제작이 시작되었습니다. 그 덕분에 케이스나 외관은 상대적으로 덜 신경쓴 티가 납니다. 내부에서 이런저런 용도로 쓰고 있던 중 한 번 보신 분들이 구매하고 싶다는 의견을 주셔서 디바이스마트를 통해 판매까지 이어지게 되었습니다. 내부 센서는 CMOS 1.3M급을 사용했으며, 전송은 640×480 해상도로 왼쪽, 오른쪽 각각 30 프레임씩 동기가 맞은 영상이 USB 2.0 포트를 통해 전달됩니다. 베이스라인은 물리적인 배치는 116mm이며, 제품마다 부착할 때 조금씩 편차는 발생하게 됩니다. 이는 캘리브레이션을 통해 보상할 수 있습니다. 보드는 밑 부분에 일반 카메라 삼각대를 부착할 수 있는 기구물이 있어 이를 부착하면 삼각대에 바로 연결할 수 있습니다. 삼각대가 아닌 다른 곳에 장착을 하는 용도로는 보드 네 귀퉁이에 M3 홀이 뚫려 있으므로 이를 활용하시면 됩니다. USB 포트에 연결하고 설치 프로그램을 설치하면, 바로 화면에 영상이 나옵니다. 렌즈는 M12 렌즈를 사용하며 촛점거리가 서로 다른 세 종류의 렌즈를 기본 제공하여 필요에 따라 선택할 수 있도록 하였습니다. 지원하는 OS는 Windows XP/Vista, win7 32bit/64bit를 지원하며, OpenCV와 연결하는 예제 코드도 제공하여 빠르게 원하시는 결과를 볼 수 있도록 하였습니다. 각각의 카메라는 노출 시간, 화이트 밸런스를 설정할 수 있으며, 그 결과들은 아래 링크에서 동영상으로 확인해 보실 수 있습니다. http://withrobot.com/category/Camera ■ OjOcam Roadmap 위드로봇(주)에서는 고성능, 고해상도 스테레오 카메라와 다채널 카메라를 지속적으로 출시할 예정입니다. 현재는 VGA급 해상도를 30프레임으로 전송하고 있습니다만, VGA급 해상도에 글로벌 셧터를 내장하고, 60프레임의 속도로 USB 3.0 인터페이스를 갖춘 OjOcamStereo-VGA60이 개발되고 있으며, 속도보다는 해상도에 중점을 둔 OjOcamStereo-QXGA15도 개발 중입니다. ■ 무료 강좌 공지 원래는 글을 통해 스테레오 이미지 처리의 기초를 잘 풀어보려고 했으나 역시나 지면을 통해 지식을 전달하는 데에 한계를 느낍니다. 직접 만지면서 영상을 보면서 작업하면 금방 이해될 것을 글로 설명하려다보니 비효율적이라는 생각이 드네요. 8월 11일 토요일 오전 10시 ~ 12시, 8월 18일 토요일 오전 10시 ~ 12시에 위드로봇(주)에서 디바이스마트 협조를 받아 OjOcamStereo-VGA30을 이용한 스테레오 영상 처리에 대한 세미나와 실습을 진행합니다. 노트북을 지참하고 오시는 분들은 OjOcamStereo-VGA30을 직접 연결하여 영상을 확인해 보실 수 있으며, 캘리브레이션 및 거리 영상을 추출하는 코드를 직접 돌려보며 스테레오 영상 처리 분야에서 이슈가 되는 부분을 직접 경험하실 수 있을 것입니다. 공간은 한정되어 있어 10명만 참석하실 수 있는데, 참석을 요청하시는 분이 많으시면 추후 추가 세미나 일정을 잡도록 하겠습니다.
|